Regla de Cramer

Cramer fue un matemático suizo nacido en Ginebra que mostró gran precocidad en matemáticas. A los 18 años recibió su doctorado y a los 20 ya era profesor en la Universidad. A día de hoy su nombre es muy escuchado gracias al método que dejó, un teorema que suele ser muy utilizado por los alumnos de segundo de bachillerato. 

Gabriel Cramer - Autor Desconocido -  Dominio Público

La regla de Cramer permite resolver los sistemas de ecuaciones lineales que cumplen ciertas condiciones utilizando los determinantes. En la entrada de hoy sólo vamos a ver este método aplicado a los Sistemas Compatibles Determinados. 

La regla de Cramer dice: "Un sistema de n ecuaciones con n incógnitas, en el cual el determinante de la matriz de los coeficientes es distinto de cero, admite una solución y sólo una, es decir, es un sistema compatible determinado".

Veamos cómo se calcula la solución utilizando el método de Cramer:

Consideramos un sistema de n ecuaciones y n incógnitas:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

La expresión matricial del sistema es:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

La solución del sistema vendría dada por:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Donde :

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Es el determinante que resulta de sustituir en la columna i-ésima por la columna de los términos independientes, siendo i=1,2,...n

Veamos ahora un ejemplo de resolución de un sistema lineal de 3 ecuaciones y 3 incógnitas utilizando el método de Cramer:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

En primer lugar escribiremos nuestro sistema en forma matricial y calcularemos el determinante de la matriz de coeficientes:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Como este determinante es distinto de 0, nos indica que el rango de la matriz es 3 y por lo tanto el sistema es Compatible Determinado (Véase la entrada Rouché-Frobenius) y válido para aplicar el método.

Por tanto, la solución del sistema vendrá dada por:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

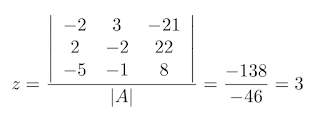Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Como se puede comprobar, el método de Cramer es un método muy sencillo si se domina el cálculo de determinantes. Desde aquí os animo a que lo pongáis en práctica y lo uséis como un método habitual para resolver los sistemas que se os proponen. Os dejo aquí un enlace con ejercicios para que practiquéis.

Referencias:

Wikipedia

Teorema de Rouché-Frobenius

Hay un concepto referido a los sistemas que genera risas y confusión la primera vez que se escucha, se trata de la discusión de sistemas, y no...no se trata de ningún enfrentamiento entre sistemas. Discutir un sistema es estudiar el número de soluciones que posee, para ello disponemos de varias herramientas, una de ellas será la protagonista de nuestra entrada de hoy. ¡Vamos a ello!En una entrada anterior vimos la notación matricial de un sistema lineal, así como las definiciones de matriz de coeficientes y matriz ampliada, hoy vamos a necesitarlas para hablar del teorema de Rouché-Frobenius. Este teorema nos permitirá saber si el sistema tiene o no tiene solución estudiando los rangos de la matriz de los coeficientes y de la matriz ampliada.

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Si tenemos un sistema de m ecuaciones con n incógnitas y consideramos su forma matricial,    Ax = b, siendo la dimensión de A mxn y la de x y b nx1, el teorema establece que la condicion necesaria y suficiente para que el sistema sea compatible es que los rangos de las matrices A y A* sean iguales.

• Si rg(A) = rg(A*) = n (número de incógnitas), el sistema es compatible determinado: el sistema tiene una única solución.

• Si rg(A) = rg(A*) < n, el sistema es compatible indeterminado: tiene infinitas soluciones.

• Si rg(A) ≠ rg(A*), el sistema es incompatible, es decir, no tiene solución.

Para los que no recordéis cómo se calculaba el rango de una matriz os dejo el enlace a una entrada de mi compañera Amalia en la que os explica cómo calcularlo.

Referencia:

Matemáticas aplicadas a las ciencias sociales II, 2 bachillerato. Luis Sanz, Fernando Alcaide, Joaquín Hernandez, María Moreno, Esteban Serrano. Ed: SM

Ejemplo resolución de sistemas por el método de Gauss

En la anterior entrada vimos en qué consistía el método de Gauss, hoy vamos a ver un ejemplo de cómo aplicamos este método resolviendo el siguiente sistema: 

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Como ya vimos, se trata de transformar el sistema en uno equivalente escalonado. Empezamos expresando nuestro sistema en forma matricial: 

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Ahora haremos las transformaciones necesarias para que nuestra matriz sea escalonada.

Sustituimos la fila 2 por la fila 2 menos 3 veces la fila 1 y la fila 3 por la fila 3 menos 2 veces la fila 1, obtenemos el siguiente resultado: 

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Si ahora sustituimos la fila 3 por 7 veces la fila 3 menos 3 veces la fila 2 llegamos a la siguiente matriz: 

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

De esta manera, ya tendríamos transformado el sistema en un sistema escalonado. No hay ninguna fila nula y el último elemento de la última fila de la matriz de la parte izquierda es no nulo, por tanto el sistema no es incompatible. El número de filas no nulas coincide con el número de incógnitas, el sistema es compatible determinado.

Como ya vimos, la solución se obtiene despejando y sustituyendo sucesivamente de abajo a arriba:

2z = -6 -> z = -3

Sustituyendo z = -3 en la segunda ecuación obtenemos: -7y + 4(-3) = -26 -> y = 2

Finalmente, sustituimos z e y en la primera ecuación y obtenemos que x = -2

Y para que practiquéis lo aprendido, os dejo un enlace con ejercicios:
Ejercicios sistemas lineales por el método de Gauss

Referencias:

Matemáticas aplicadas a las ciencias sociales II, 2 bachillerato. Luis Sanz, Fernando Alcaide, Joaquín Hernandez, María Moreno, Esteban Serrano. Ed: SM

Método de Gauss

Antes de empezar con el Método de Gauss vamos a repasar el concepto de sistema escalonado. Un sistema escalonado es aquel en el que cada ecuación tiene una incógnita menos que la anterior.

Ejemplo de sistema escalonado:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

El método de Gauss consiste en sustituir el sistema dado por otro equivalente, aplicando las transformaciones necesarias, hasta conseguir un sistema escalonado. Una vez lleguemos a la forma escalonada tendremos tres casos posibles:

• Si alguna de las filas que quedan está formada por todo ceros excepto el término independiente, que es distinto de cero, el sistema es incompatible y no tiene solución.
• Si no es incompatible, se consideran el número de filas no nulas que quedan y el número de incógnitas:
• Si el número de filas no nulas coincide con el de incógnitas, el sistema es compatible determinado, y su única solución se puede obtener de forma muy sencilla resolviendo de abajo a arriba el sistema escalonado.
• Si el número de filas no nulas es menor que el de incógnitas, el sistema es compatible indeterminado, y sus infinitas soluciones se obtienen con la ayuda de tantos parámetros como diferencia haya entre el de incógnitas y el número de filas no nulas. Se consideran como parámetros las incógnitas que no son principales y se pasan al otro miembro de cada una de las ecuaciones. A continuación se resuelve despejando de abajo a arriba.

Algoritmo de eliminación de Gauss-Jordan

1. Ir a la primera columna no cero de izquierda a derecha.
2. Si la primera fila tiene un cero en esta columna, intercambiarlo con otra que no lo tenga.
3. Luego, obtener ceros debajo de este elemento delantero, sumando múltiplos adecuados de la fila superior a las filas de debajo de ella.
4. Dejamos fija la fila superior y repetimos el proceso anterior con la submatriz restante. Repetir con el resto de filas hasta llegar a una matriz escalonada

Referencias:

Wikipedia

Apuntes Marea Verde

Matemáticas aplicadas a las ciencias sociales II, 2 bachillerato. Luis Sanz, Fernando Alcaide, Joaquín Hernandez, María Moreno, Esteban Serrano. Ed: SM

Expresión matricial de un sistema de ecuaciones y sistemas equivalentes

Seguimos con el repaso de algunos conceptos útiles para la resolución de un sistema de ecuaciones, esta vez nos toca recordar su forma de expresión matricial. 

Si tenemos un sistema de m ecuaciones lineales con n incógnitas: 

Recorte de pantalla de Wikipedia (Sistemas de ecuaciones lineales) CC BY-SA 3.0. Fte. Elaboración propia

Podemos escribirlo de la forma Ax = b, donde A (matriz de coeficientes) será una matriz mxn, x (vector de incógnitas) un vector columna con n elementos y b (vector de términos independientes) también un vector columna con m elementos.  
Veamos cómo sería en el caso general de un sistema de 3 ecuaciones con 3 incógnitas:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Llamamos matriz ampliada, A*, a la matriz formada por la combinación de A y b:

Recorte de LaTeX de elaboración propia CC BY-SA 4.0 

Sistemas Equivalentes

Otro de los conceptos que vamos a repasar en esta entrada es el de Sistemas Equivalentes. Dos sistemas con el mismo número de incógnitas, aunque no tengan el mismo número de ecuaciones, se dice que son equivalentes si tienen las mismas soluciones, es decir, toda solución del primero es solución del segundo, y viceversa.

Si en un sistema de ecuaciones lineales cualquiera se realiza alguna de las siguientes transformaciones, se obtiene siempre un sistema equivalente:

• Cambiar el orden de las ecuaciones.
• Multiplicar o dividir los dos miembros de la ecuación por un número distinto de cero.
• Sumar a una ecuación otra multiplicada por un número.
• Eliminar una ecuación que es combinación lineal de otras.

Referencias:
Wikipedia
Apuntes Marea Verde
Matemáticas aplicadas a las ciencias sociales II, 2 bachillerato. Luis Sanz, Fernando Alcaide, Joaquín Hernandez, María Moreno, Esteban Serrano. Ed: SM

Sistemas de ecuaciones lineales

Hoy vamos a hablar de los sistemas de ecuaciones lineales. Para los estudiantes de 2º de bachillerato los sistemas de ecuaciones lineales son ya viejos conocidos pero en esta entrada vamos a empezar repasando algunos conceptos.

Un sistema lineal es un sistema en el cual cada ecuación que lo forma es de primer grado. Resolver el sistema consiste en encontrar los valores de las variables que cumplen las ecuaciones que lo forman.

Clasificación de sistemas lineales

Podemos clasificar los sistemas según el número de soluciones que tengan de la siguiente forma:

• Si el sistema tiene solución diremos que se trata de un Sistema Compatible. Si esta solución es única diremos que es un Sistema Compatible Determinado y si tiene infinitas soluciones lo llamaremos Sistema Compatible Indeterminado.
• Si por el contrario, no tiene solución, diremos que se trata de un Sistema Incompatible.

Geométricamente los sistemas incompatibles son rectas, planos o hiperplanos que se cruzan sin cortarse, los sistemas compatibles determinados son rectas planos o hiperplanos que se cortan en un único punto y los sistemas compatibles indeterminados son planos o hiperplanos que se cortan a lo largo de una recta.

Recorte de LaTeX de elaboración propia CC BY-SA 4.0